An Introduction to Elliptic Curve Cryptography: With Math!

by

Modern cryptography is a very murky subject for many people, so today I will try to explain to you one of the more complex subjects, Elliptic Curves. Many of you may have heard their name before, but likely don’t know much about them beyond that. To begin, I will describe what an elliptic curve is.

An elliptic curve is an equation in the form Y^2=X^3+AX+B where 4A^4+27B^2\ \neq\ 0.
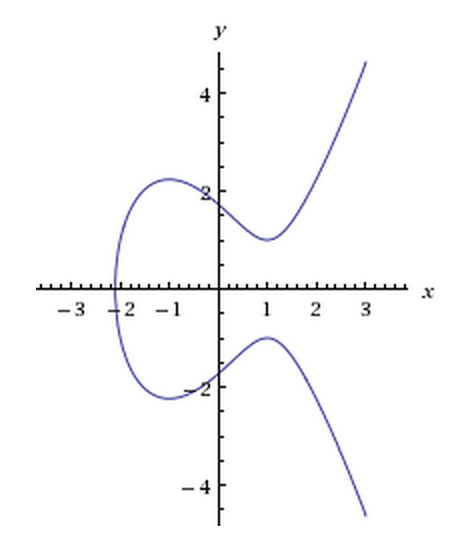
If you refer to figure 1, you can see a handy graph of what one elliptic curve looks like.

Example graph of an Elliptic Curve.

Now, elliptic curves are useful for crypto because they have some useful properties. They have an identity element (P \oplus 0 = P), the have an inverse (P \oplus P' = 0), they are associative (P \oplus Q = Q \oplus P), and they are commutative (P \oplus (Q \oplus R) = (P \oplus Q) \oplus R). This means they form an Abelian group. Which means that they behave “nicely” for how we want to use them.

In the prior section, I listed some equations that likely looked kinda familiar, but also weird because of the \oplus symbol. This symbol is similar to + that you know, but is the analogue for adding two points on an elliptic curve. To add two points on an elliptic curve, you draw a line between them, then find the 3rd point on that line that intersects the curve. Then you mirror that point across the x-axis and that point on the curve is the result of that addition. If that description didn’t make the most sense, refer to figure 2 to see a graphic depiction.

Animated example of Elliptic Curve addition.

However, there are some corner cases we also need to address. What if the line between the two points doesn’t intersect the curve again? Then we say that the third point is 0, which can be thought of as a point at infinity (figure 3).

Animated example of Elliptic Curve addition using point at infinity.

Lastly, what if we add the same point to itself. This can be done by using the line tangent to the point, and then finding the 3rd point the same way as before (figure 4).

Animated example of Elliptic Curve addition using point at infinity.

Now that we understand what an elliptic curve is, we must address the motivation for using an elliptic curve for crypto. In traditional public key crypto, the name of the problem that makes them hard to crack is called the Discrete Log Problem. There is an analogous problem on an elliptic curve named the Elliptic Curve Discrete Log Problem. Now even though they are related problems, the time complexity of solving the DLP is less than the time complexity of solving the ECDLP. O( p^{\epsilon}\textrm{ for every }\epsilon > 0) vs O(\sqrt{P}\textrm{ on }F_p) respectively. Thus, elliptic curve crypto is much harder to brute force a solution.

Lastly, I will provide an example of how elliptic curves can be used for crypto. I will begin with describing the traditional Diffie-Hellman key exchange involving two people, Alice and Bob.

To do D-H key exchange, Alice and Bob both public agree upon two numbers g and p that they will share. Then, Alice generates A based on her secret number \alpha and Bob generates B based on his secret number \beta using the equations A \equiv g^{\alpha} (mod\ p) and B \equiv g^{\beta} (mod\ p) respectively. They then publicly exchange A and B. Alice then computes B^{\alpha} (mod\ p) and Bob computes A^{\beta} (mod\ p). However, these can be rewritten as (g^{\beta})^{\alpha} (mod\ p) and (g^{\alpha})^{\beta} (mod\ p) which are the same (because these operations are commutative). Thus, they have a shared number, but an outsider must solve the DLP for either A or B using g and m to recover \alpha or \beta which can then be used to find this secret shared number. This is visually demonstrated in figure 5

Animated example of Elliptic Curve addition using point at infinity.

Now, we can write the elliptic curve analog by replacing the operations a^b (mod\ p) with nP (mod\ p).

Thus, D-H key exchange using elliptic curves looks as follows. Alice and Bob agree upon a public point P on shared publicly known curve C. Then Alice generates Q_a based on her secret number n_a and Bob generates Q_b based on his secret number n_b using the equations Q_a = n_aP (on C) and Q_b = n_bP (on C). They then publicly exchange Q_a and Q_b. Alice then computes n_aQ_b (on C) and Bob computes n_bQ_a (on C). These can be rewritten as n_a(n_bP) and n_b(n_aP) (both on c). Again, these are the same it is commutative. Again, they have a shared number (technically a point, but it can be converted to a number), but an outsider must solve the ECDLP for either Q_a or Q_b using P and the curve C in order to recover n_a or n_b which can then be used to find the shared secret. You can also refer to figure 6.

Animated example of Elliptic Curve addition using point at infinity.

Now that you’ve got a basic understanding of elliptic curves, it is important to remember, “with great power comes great responsibility.” It is almost never correct to write your own crypto algorithms. You should usually defer to using public and well known implementations. It is very common create bugs in your code that weaken your implementation while still allowing it to “work”.

Leave a Reply

Your email address will not be published. Required fields are marked